A few words

In the near future, I’d like to lead a series of creative coding workshops for youth. We’ll be drawing various shapes and creating animations in the browser, most likely using p5.js. However, I need to brush up on my skills a bit.

I’ve started with a simple problem: drawing a line on a pixel grid, and I’ve become a bit frustrated. Many resources discussing this topic start with derived math equations, while I need to grasp the intuition first. Here’s how I see it.

The task

Draw a straight line on the screen from pixel A to pixel B. Not with a pen though. Computer screens have milions of pixels nowadays, so let’s simplify things a bit. Consider the following conditions:

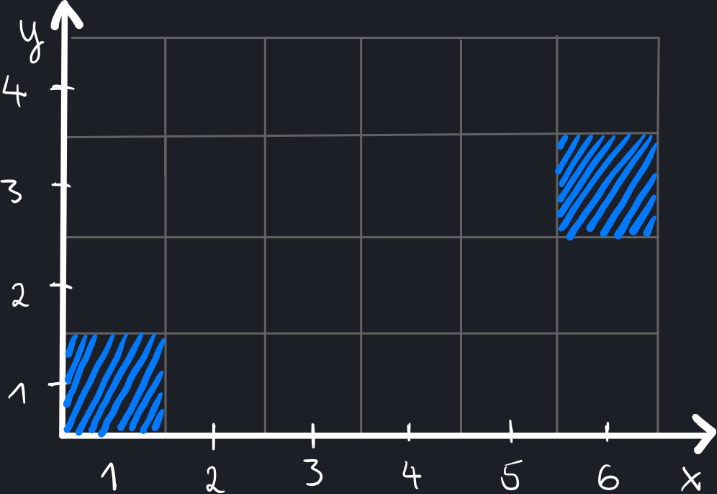
Grid: 6x4
Pixel A: (1, 1)
Pixel B: (6, 3)

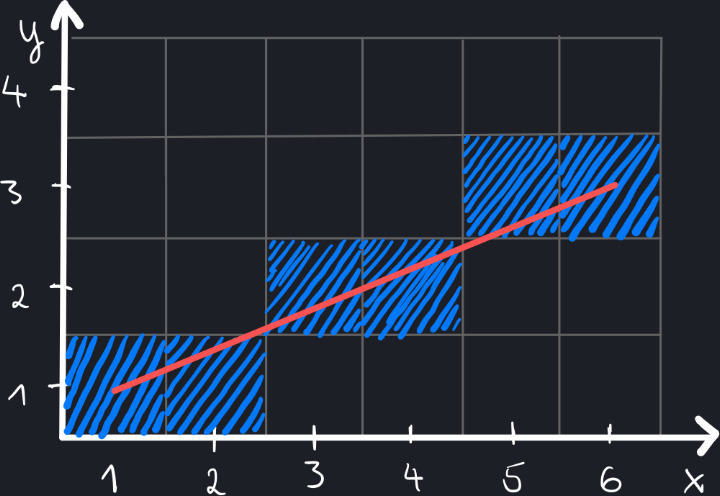
Each square represents one pixel on the screen. Let’s fill our A and B pixels with color:

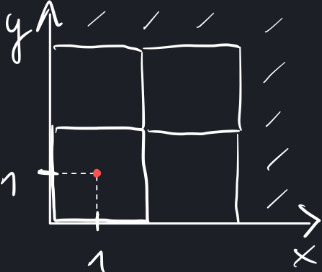
Notice that every integer point lies exactly at the center of a pixel. For instance, the point (1, 1) is at the center of pixel A. This is illustrated by the red dot below:

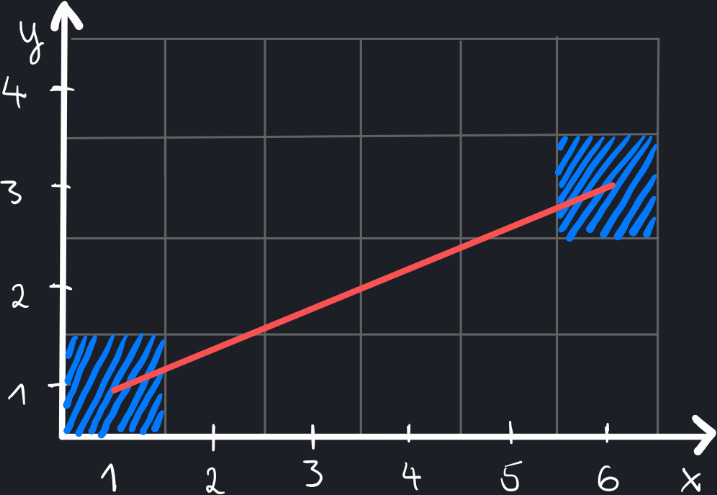
Alright, so how do we draw the line now? Which pixels on the grid should we color? Remember that we must color entire pixels or none; we can’t color half or a third of a pixel.

Let’s draw a red helper line that passes through the start and end points, or in other words, through the centers of pixel A and pixel B.

Now, looking at each column at a time, decide which pixel (relative to its center) is closer to the line.

In the second column (x = 2), the pixel below the line is closer.
In the third column (x = 3), the pixel above the line is closer.
…and so on.

I’ve marked the closer distance with a yellow color, and the longer distance with a gray color:

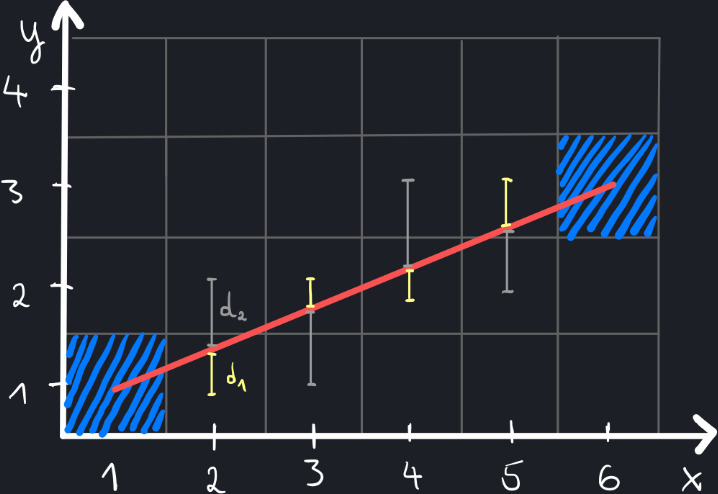
Color the pixels that are closer to the helper line:

That’s it. The line can’t be any straighter, believe me. You now understand the idea behind Bresenham’s line algorithm.

Math

I encourage you to derive the equations on a piece of paper. I don’t want you to come up with everything on your own, just do it while looking at this elegant derivation presented by Ela Claridge from the University of Birmingham.

Play

Feel free to click around. Thank you for reading.